Related Resources: calculators
Water Vapor Saturation Pressure Formulae and Calculator
Thermodynamics and Heat Transfer
Water Vapor Saturation Pressure
Increasing temperature of liquid (or any substance) enhances its evaporation that results in the increase of vapor pressure over the liquid. By lowering temperature of the vapor we can make it condense back to the liquid. These two phase transitions, evaporation and condensation, are accompanied by consuming/evolving enthalpy of transition and by a change in entropy of the material.
The water vapor saturation pressure is required to determine a number of moist air properties, principally the saturation humidity ratio. Saturated water vapor pressure is a function of temperature only and independent on the presence of other gases. The temperature dependence is exponential. For water vapor the semi empirical dependence reads as :
Equation 1
pw, s = eA + B/T + C lnT +Dt
Where:
pw, s = water vapor saturation pressure (Pa)
T = Temperature in Kelvin, K = °F + 255.927778
A = 77.34,
B = -7235,
C = - 8.2,
D = 0.005711,
e =
2.718281828,
t = saturation temperature
Reference:
Lecture Notes
Sampo Smolander
University of Helsinki
Alternative (recommended) formula given by IPAWS R7-97(2012) and R14-08 (2011). The saturation pressure over liquid water for the temperature range of 32 to 392°F is given by:
Equation 2
ln pw, s = C8/T + C9 + C10T + C11T2 + C12T3 + C13 ln T
Where:
pw, s = saturation pressure, psia
T = absolute temperature, °R = °F + 459.67
C8 = –1.0440397 E+04
C9= –1.1294650 E+01
C10 = –2.7022355 E–02
C11 = 1.2890360 E–05
C12 = –2.478068 1 E–09
C13 = 6.5459673 E+00
The coefficients of Equations (2) were derived from the Hyland-Wexler equations, which are given in SI units.
Above the surface of liquid water there always exists some amount of gaseous water and consequently there exists a vapor pressure. When a container containing water is open then the number of the escaping molecules is larger than the number of molecules coming back from the gaseous phase (Fig. 1). In this case vapor pressure is small and far from saturation. When the container is closed then the water vapor pressure above the surface increases (concentration of molecules increases) and therefore the number of molecules coming back increases too (Fig. 2). After some time, the number of molecules escaping the liquid and that coming back becomes equal. Such situation is called by dynamic equilibrium between the escaping and returning molecules (Fig. 3). In this case, it is said that the water vapor pressure over the liquid water is saturated.
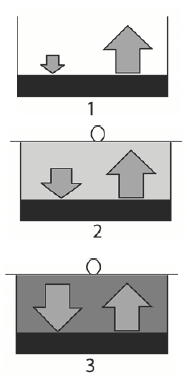
Figues 1, 2 and 3
Table 1 - Derived from Equation 2
Temperature |
Saturation Pressure |
||
˚ F |
˚ R |
psia |
Pa |
32 |
491.7 |
0.0886 |
611.21 |
44 |
503.7 |
0.1420 |
979.27 |
56 |
515.7 |
0.2220 |
1530.79 |
68 |
527.7 |
0.3392 |
2338.80 |
80 |
539.7 |
0.5074 |
3498.08 |
92 |
551.7 |
0.7439 |
5129.31 |
104 |
563.7 |
1.0709 |
7383.46 |
116 |
575.7 |
1.5151 |
10446.37 |
128 |
587.7 |
2.1093 |
14543.35 |
140 |
599.7 |
2.8926 |
19943.75 |
152 |
611.7 |
3.9110 |
26965.43 |
164 |
623.7 |
5.2183 |
35978.96 |
176 |
635.7 |
6.8765 |
47411.59 |
188 |
647.7 |
8.9562 |
61750.80 |
200 |
659.7 |
11.5374 |
79547.49 |
212 |
671.7 |
14.7095 |
101418.67 |
224 |
683.7 |
18.5720 |
128049.71 |
236 |
695.7 |
23.2345 |
160196.16 |
248 |
707.7 |
28.8168 |
198685.05 |
260 |
719.7 |
35.4495 |
244415.77 |
272 |
731.7 |
43.2735 |
298360.56 |
284 |
743.7 |
52.4405 |
361564.68 |
296 |
755.7 |
63.1126 |
435146.16 |
308 |
767.7 |
75.4625 |
520295.41 |
320 |
779.7 |
89.6731 |
618274.54 |
332 |
791.7 |
105.9380 |
730416.57 |
344 |
803.7 |
124.4604 |
858124.52 |
356 |
815.7 |
145.4541 |
1002870.48 |
368 |
827.7 |
169.1422 |
1166194.58 |
380 |
839.7 |
195.7580 |
1349704.14 |
392 |
851.7 |
225.5442 |
1555072.74 |
Related:
- Steam Tables - Thermodynamics - Thermodynamics
- Water Saturation Pressure Temperature
- Partial Pressure of Water Vapor in Saturated Air Table Chart
- Saturation Thermodynamic
- Saturated Steam Tables Imperial Units
- Saturated Steam Table Chart Metric Units
- Thermodynamic Properties Saturated Water Pressure Entry Tables
References:
- Adapted from NASA (1976).