Related Resources: calculators

Thick Walled Cylinder Stress Pressure Vessel Equations and Calculator

Pressure Vessel Design Formula and Calculators Resources

Thick Walled Cylinder Stress Pressure Vessel Equations and Calculator

Thick-walled cylinders have application in all sorts of machine elements and will be the basis for the presentation for shrink or press fits. Typically a cylinder is considered thick if the diameter is less than ten times the wall thickness.

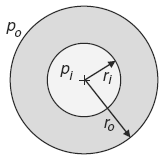
Figure 1
Geometry of a thick-walled cylinder

Preview: Thick Walled Cylinder Pressure Vessel Stress Calculator

External pressure on any thin-walled vessel causes buckling of the vessel wall long before excessive stress is reached. The study of the buckling of thin-walled vessels is very complex, and is beyond the scope of this document.

The major difference between the stresses in a thin-walled cylinder and a thick-walled cylinder is that the hoop stress, also called the tangential stress, for the thick-walled cylinder varies in the radial direction, and there is a radial stress across the thickness of the cylinder that also varies radially. Unlike thin-walled vessels, thickwalled cylinders do not tend to buckle under excessive external pressure, but merely crush.

Tangential Stress Formula:

σ_t = (p_ir²_i - p_or²_o + (p_i - p_o) (r²_i r²_o / r²)) / ( r²_o - r²_i )

If the external pressure (p_o) is zero gage, meaning atmospheric, then the tangential stress (σ_t) becomes:

σ_t = p_ir² / ( r²_o - r²_o ) [ 1 + ( r_o / r )² ]

The tangential stress (σ_t ) distribution

Figure 2
Tangential stress with p_o = 0

Note that the tangential stress (σ_t) is maximum at the inside radius and a lower value at the outside radius. Also, if the outside radius is twice the inside radius, by a few algebra steps it can be shown that the tangential stress at the inside radius is two and a half times greater than the tangential stress at the outside radius.

Radial Stress. For the geometry and pressures shown in Figure 1, the radial stress σ_r is given by:

σ_r = ( p_ir²_i - p_or²_o - (p_i - p_o) (r²_i r²_o / r²) ) / ( r²_o - r²_i )

Note that the radial stress (σ_r ) is a maximum at the inside radius and zero at the outside radius. Also notice that there are no arrows on the lines displaying the distribution like there were for the tangential stress distribution. This is because the radial stress is in the radial direction, so the length of the plain lines on the distribution curve represent the magnitude of the radial stress. (The arrows on the tangential stress distribution curve represented both magnitude and direction.)

Where:

p_i = internal pressure (psi, MPa),
p_o = external pressure (psi, MPa), atmospheric = 0,
r_i = inside radius (in, m),
r_o = external radius (in, m),
r = some radius within the material between r_i and r_o

Related:

• Pressure Vessel External Pressure Calculations
• Pressure Vessel, Thin Wall Longitudinal Stress Calculator
• Pressure Vessel, Thin Wall Hoop and Longitudinal Stresses Equation and Calculator
• Pressure Vessel Design Calculations Handbook
• Identifying and Reducing Stresses in Pressure Vessels

Source:

Marks' Calculations for Machine Design,
Thomas H. Brown, Jr. Ph.D., PE
Faculty Associate
Institute for Transportation Research and Education
NC State University
Raleigh, North Carolina